Efecto Túnel Cuántico
En física clásica si tenemos una partícula cuya energía es mayor que Vo entonces se podrá mover sin problema en todo el eje X.
Figura 1. Barrera de potencial.
Si la partícula tiene una energía menor que Vo (fig. 1) no podrá superar la barrera y quedará confinada en la parte izquierda de la barrera. En cambio en MC, las partículas cuánticas están descritas por una función de onda ψ , que contiene la información acerca de la probabilidad que tiene la partícula de ser encontrada en una posición determinada de forma que el cuadrado de la función de onda es iguala a uno.
Cuando describimos una partícula cuántica que se encuentra con una barrera de potencial y resolvemos el problema encontramos que aunque dicha partícula no tenga la energía suficiente como para “saltar” la barrera hay una pequeña probabilidad de encontrar la partícula al otro lado.
Cuando describimos una partícula cuántica que se encuentra con una barrera de potencial y resolvemos el problema encontramos que aunque dicha partícula no tenga la energía suficiente como para “saltar” la barrera hay una pequeña probabilidad de encontrar la partícula al otro lado.
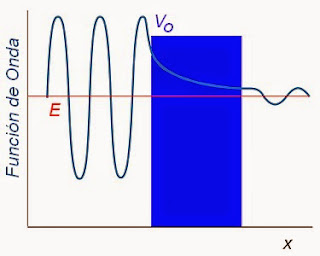
Figura 2. Onda Transmitida.
La función de onda contiene las partículas incidentes y reflejadas. La parte reflejada disminuye exponencialmente (fig. 2) de forma que no alcanza el cero en x=a, sino que continúa a la derecha de dicho punto con una cierta amplitud. La función de onda a la derecha del punto a, representa las partículas transmitidas. En definitiva, la partícula descrita por la función de onda ψ que tiene una energía menor que la barrera de potencial es capaz de saltar la barrera.
Como se ve en la figura la amplitud de la onda en la parte transmitida es menor. La amplitud está relacionada con el cuadrado de la función de onda, y eso es la probabilidad de encontrar la partícula en una determinada posición. Por lo tanto, como se ve en la figura, la probabilidad de encontrar a la partícula al otro lado de la barrera es muy pequeña.
Como se ve en la figura la amplitud de la onda en la parte transmitida es menor. La amplitud está relacionada con el cuadrado de la función de onda, y eso es la probabilidad de encontrar la partícula en una determinada posición. Por lo tanto, como se ve en la figura, la probabilidad de encontrar a la partícula al otro lado de la barrera es muy pequeña.
Conservación del Momento Angular.
En una exhibición de patinaje artístico, se observa que cuando los patinadores acercan los brazos al cuerpo su velocidad de rotación ω aumenta y el momento de inercia I disminuye, lo que demuestra la ley de conservación del momento angular.
Figura 3. Conservación del momento angular.
Por otra parte, la energía cinética de rotación es mayor cuando mayor es la velocidad de rotación. Ese aumento de energía se produce a expensas de una disminución de la energía potencial interna con lo que la energía mecánica no cambia.
Podemos suponer que el patinador es un autómata con un resorte interno, con un funcionamiento similar al de un reloj de cuerda; los músculos del patinador serían el equivalente del resorte. Éste se mantiene elongado cuando el patinador tiene los brazos extendidos, los cuales se acercan al cuerpo cuando el resorte recupera su forma original. De este modo disminuye la energía potencial interna almacenada en el resorte.
Ocurre exactamente lo mismo en el efecto túnel. A partir de la hipótesis de que el Universo y las partículas están formadas por átomos de espacio-tiempo de cuatro dimensiones se deduce que las partículas son átomos de Planck que están en el estado de mínima energía. Esta energía es debida a la rotación del átomo de Planck de cuatro dimensiones. Este giro arrastra a los átomos de espacio-tiempo adyacentes hasta una distancia igual a su longitud de onda en reposo.
Efecto túnel clásico.
Supongamos que no podemos ver al patinador, pero podemos medir su energía cinética de rotación. El patinador está en todo momento con los brazos extendidos, a menos que haya un obstáculo Después de realizar algunas medidas desde la grada, pero variando la distancia (x1, x2, x3) a la que realizamos la medida, se llega a la conclusión errónea de que la energía cinética de rotación (Em fig. 4) es una propiedad intrínseca del patinador. Patinador que no podemos ver. Supongamos además, que a medida que mejora la tecnología nos acercamos más al patinador. Para poder seguir girando, el patinador acerca los brazos al cuerpo, de forma que al medir la energía a una distancia inferior a la longitud de sus brazos observamos como la energía E’ ha aumentado. La energía máxima será EM, cuando el patinador tenga los brazos pegados al cuerpo. En la gráfica L representa la longitud de los brazos del patinador.
Figura 4. Energía cinética de rotación del patinador en función de la distancia de medida.
Ocurre exactamente lo mismo en el efecto túnel. A partir de la hipótesis de que el Universo y las partículas están formadas por átomos de espacio-tiempo de cuatro dimensiones se deduce que las partículas son átomos de Planck que están en el estado de mínima energía. Esta energía es debida a la rotación del átomo de Planck de cuatro dimensiones. Este giro arrastra a los átomos de espacio-tiempo adyacentes hasta una distancia igual a su longitud de onda en reposo.
Si la partícula está lejos de la barrera de potencial de forma que la distancia igual o mayor que su longitud de onda (fig. 5 a), entonces su energía es inferior a la de la barrera de potencial.
A medida que la partícula se acerca a la barrera de potencial, de la misma forma que el patinador encoge los brazos, la partícula aumenta su rotación (fig. 5 b) con lo que su energía aumenta, hasta que su energía alcanza el valor Vo (fig. 5 c) y supera la barrera. Una vez superada la barrera la partícula vuelve al estado de mínima energía (fig. 5 d).
Las partículas son átomos de Planck de cuatro dimensiones que están en el estado de mínima energía.
Cualquier perturbación hace que la partícula varíe su energía, pero conservando el momento y vuelve rápidamente al estado de mínima energía.
El problema radica en suponer que la masa de la partícula es una propiedad intrínseca de la materia, ya que las teorías actuales (mecánica cuántica y relatividad general) no permiten explicar: ¿Qué es la masa?
La física actual no explica que es la masa, sencillamente porque no tiene ni idea. Decir que es una propiedad intrínseca de la materia es lo mismo que decir que los rayos y truenos son debidos al dios Thor.
No existe una probabilidad de encontrar la partícula al otro lado de la barrera, simplemente porque la función de onda, como veremos el mes próximo, no tiene nada que ver con la probabilidad. La energía de la partícula aumenta, de la misma forma que aumenta la energía de un patinador, y es capaz de superar la barrera si se acerca lo suficiente.