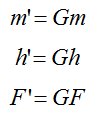En la física actual, la masa se define como la cantidad de materia de un cuerpo. La masa es una magnitud física fundamental que expresa la inercia o resistencia al cambio en el movimiento de un cuerpo. Es una propiedad intrínseca de las partículas.
La masa inercial se define a partir de la segunda ley de Newton, de
manera que al aplicar una fuerza a un objeto se produce una aceleración. Al
cociente entre la fuerza aplicada (F) y la aceleración producida (a) se le
denomina masa inercial (m)
Todas las magnitudes mecánicas se pueden definir en función de
masa, longitud y tiempo. En el sistema internacional, la unidad de masa es el
kilogramo.
En 1795, durante la Revolución francesa, se utilizaba el gramo como la masa de un centímetro
cúbico de agua destilada a una atmósfera de
presión y a la temperatura de 3,98 ºC,
correspondiente al punto de fusión del hielo.
La unidad
básica de masa en el Sistema Internacional de
Unidades es el kilogramo, que corresponde a un litro de agua. Pero debido a que la densidad del agua varía con la presión
atmosférica, se utiliza como referencia una masa patrón. Dicha masa patrón está
formada por un cilindro de platino e iridio (90% y 10%,
respectivamente), que se guarda en la Oficina Internacional de Pesos y
Medidas (BIPM) en Sèvres, cerca de París.
Hay prototipos nacionales, que son copias del
kilogramo patrón y se comparan con el prototipo de París. Sin embargo, el
prototipo internacional del kilogramo, al compararlo con las copias parece
haber perdido cerca de 50 microgramos en los últimos 100 años.
Por lo tanto, la física actual no explica qué es la masa. Simplemente da
dos formas de medir algo que denominan masa, y se asigna la unidad de masa, el
kilogramo, a un litro de agua. De esa forma se tiene una referencia patrón.
Masa inercial.
La masa inercial se define a partir de la segunda Ley de Newton:
Fuerza = masa x aceleración
Cuando se aplica una fuerza a un decímetro cúbico de agua se produce una
aceleración. Si se aplica la misma fuerza a un decímetro cúbico de hierro se
produce una aceleración distinta a la del agua. Para explicar esa diferencia,
los físicos inventaron el concepto, que no realidad física, de masa inercial.
Lo que se observa es que ambas masas ocupan un mismo volumen, pero su aceleración
es diferente. Masa = fuerza/aceleración es sólo un número.
Masa
Gravitatoria.
La masa gravitatoria se define a partir de la ley de Gravitación de
Newton. Colocamos un decímetro cúbico de agua en un dinamómetro y medimos la
fuerza. Si ahora colocamos un decímetro cúbico de hierro en un dinamómetro y
medimos la fuerza, se observa que en este caso la fuerza es mayor. Para
explicar esa diferencia de fuerzas, los físicos inventaron el concepto, que no
realidad física, de masa gravitatoria. Por lo tanto, la masa gravitatoria es
sólo un número que produce una atracción a otro número de acuerdo con la ley de
Gravitación de Newton.
¿Qué
es la masa?
En la definición de masa inercial se mide la aceleración (espacio/tiempo
al cuadrado) de un decímetro cúbico de
agua. En la definición de masa gravitatoria se mide el desplazamiento
del agua (aguja del dinamómetro). Por lo tanto en ambos casos lo que se mide es
espacio y tiempo.
De forma arbitraria, se asigna el kilogramo a la masa de un decímetro
cúbico de agua bajo determinadas condiciones. Ya los antiguos romanos usaban la
libra como unidad de peso (masa), en sus transacciones comerciales.
Ni Newton, ni los antiguos romanos sabían que tanto el agua como el hierro
y en general la materia están formadas por partículas (electrones y quarks) más
pequeñas que ocupan un volumen y que además se mueven formando átomos.
Para un mismo volumen, la cantidad de electrones y quarks que hay en el
interior de ese volumen, varía en función del objeto. Además también sabemos
que los electrones y quarks se están moviendo en el interior de los átomos. Por
lo tanto, la masa es el espacio en movimiento o simplemente espacio, que ocupan
las partículas en el interior de un volumen dado. Cuanto mas espacio esté
ocupado por las partículas mas masa tiene el objeto, para un mismo volumen. La
masa, es un concepto derivado del espacio-tiempo, no es un concepto fundamental
o intrínseco como afirma la física ortodoxa.
Desde el punto de vista tecnológico el concepto de peso o masa es
necesario, para distinguir por el precio, un kilo de azúcar de un kilo de sal.
¿Masa o espacio en movimiento?
Si la masa es el espacio en movimiento, se necesita
ahora una forma de medir la masa. Para ello, podemos hacer un cambio de
variables.
En donde m es masa, F fuerza, G es la constante de gravitación y h la constante de Planck
|
SI |
Símbolo |
Valor |
Unidades |
Dimensiones |
|
Masa |
m |
1 |
kg |
M |
|
Cte. de Gravitación |
G |
6.67408 10-11 |
m3 kg-1 s-2 |
L3 M-1 T-2 |
|
Cte. de Planck |
h |
|
kg m2 s-1 |
L2 M T-1 |
|
Fuerza |
F |
1 |
kg m s-2 |
L M T-2 |
|
Nuevo SI |
Símbolo |
Valor |
Unidades |
Dimensiones |
|
Masa |
m’ |
6.67408 10-11 |
m3 s-2 |
L3 T-2 |
|
Cte. de Gravitación |
G |
----- |
----- |
----- |
|
Cte. de Planck |
h’ |
|
m5 s-3 |
L5 T-3 |
|
Fuerza |
F’ |
6.67408 10-11 |
m4 s-4 |
L4 T-4 |
L = longitud; M = masa, T= tiempo, kg kilogramos, m
metros y s segundos
Con lo que la constante de gravitación G ya no es necesaria y el kilogramo
desaparece del Sistema Internacional de Unidades
La segunda ley de Newton no varía. Si a un litro de
agua le asignamos el valor de 6.67408 10-11 m3 s-2 resulta que la
fuerza necesaria para que se produzca una aceleración de 1 m/s2 es
de 6.67408 10-11
m4 s-4
En la gravitación de Newton desaparece la constante de Gravitación G, quedando de la forma siguiente:
En este caso dos volúmenes de agua de 1 litro cada
uno, producen una fuerza de atracción entre ellos de 6.67408 10-11 m4 s-4.
Si hacemos G=1,
resulta que:
6.67408 10-11 m3
kg-1 s-2 = 1
De donde:
1 kg = 6.67408 10-11 m3 s-2
Lo que indica que la masa ocupa un volumen, como se
desprende de la propia definición de masa. Pero además, aparece el tiempo al
cuadrado en el denominador, lo que indica que en ese volumen hay además dos
frecuencias, es decir, dos rotaciones. Lo que está de acuerdo con mi hipótesis
de que las partículas están constituidas por esferas de espacio de cuatro
dimensiones, con un diámetro igual a la longitud de Planck, con dos posibles
rotaciones [1]
Por otra parte, Januz Kowalski, llega a una conclusión similar y deduce la masa en
función de la longitud de Planck [2].
Según la física actual las partículas elementales
adquieren masa mediante el mecanismo de Higgs. Es decir, las partículas
puntuales adquieren espacio (masa) mediante la interacción con el campo de
Higgs para continuar siendo puntuales. Por lo tanto el mecanismo de Higgs, no
tiene nada que ver con la masa, es simplemente una formula matemática para
dejar satisfechos a la mayoría de los físicos.
En definitiva la constante de gravitación es una
construcción humana, que no tiene nada que ver con el universo. Resulta
evidente que el valor de la constante de gravitación depende del patrón de masa
elegido y de las definiciones de longitud y tiempo. Si como unidad de masa se
hubiera elegido el mismo volumen (1 dm3) de hierro, el valor de G
sería menor. Si hubiéramos definido el segundo como la centésima parte de un
minuto, el valor de G sería mayor.
Para Duff, las
constantes dimensionales, tales como ħ, c, G, e, k, son construcciones humanas que no varían en
el tiempo. “La posible variación en el tiempo de las constantes
fundamentales de la naturaleza adimensionales, como la constante α de
estructura fina, es un tema legítimo de investigación física. Por el contrario,
la variación en el tiempo de las constantes dimensionales, como ħ, c, G, e, k, ... que son simplemente
construcciones humanas cuyo número y valores difieren de una elección de
unidades a la siguiente, no tiene ningún significado operativo” [3].
Conclusión
En definitiva, la masa no es una magnitud física
fundamental, como afirma la física actual, ya que se puede obtener en función
de otras. Por lo tanto, la masa es una magnitud derivada del espacio y tiempo,
siendo la constante de gravitación el factor de conversión entre el volumen
ocupado por el objeto, dentro de un volumen externo dado, en algo que denominamos masa.
Sin embargo, de la misma manera que el volumen se
puede medir en litros, barriles, galones, metros cúbicos, etc., la masa se
puede medir en metros cúbicos / segundo al cuadrado o en kilogramos, tal como
estamos acostumbrados. Lo importante no es la unidad de medida; lo importante
es que cualquier masa, incluidas las partículas elementales, ocupan un volumen
y por lo tanto tienen impulso y posición perfectamente definidas, aunque estas dos
variables no se puedan medir simultáneamente.
El valor de G no es aleatorio, sino que depende de
las unidades de longitud masa y tiempo elegidas.
[1] https://www.gsjournal.net/Science-Journals-Papers/Author/1743/Jose%20Garrigues,%20Baixauli
[2]
https://kowalski-physics.blogspot.com/2021/01/natural-geometric-unit-system-and.html
[3] Duff, M.
J. (2002). Comment
on time-variation of fundamental constants.
arXiv: hep-th / 0208093