Resumen de Formulas
Los ordenadores se utilizan en aspectos tan diversos como: negocios,
banca, seguros, mercadeo, educación, salud, diseño de ingeniería, comunicación,
gobierno, inteligencia artificial, etc.
Pero la aplicación más interesante, desde el punto de vista físico,
es la computación científica, donde se emplean técnicas
numéricas para resolver problemas científicos. La computación científica
abarca diferentes campos, tales como: simulaciones numéricas y análisis de
datos. Para lo cuál se emplean diferentes métodos y algoritmos, entre los que
cabe destacar:
- Análisis numérico.
- Aplicación de series de
Taylor como series convergentes y asintóticas.
- Método de Runge-Kutta para
resolver ecuaciones diferenciales ordinarias.
- Método de Montecarlo.
- Álgebra lineal numérica.
La computación científica se
estudia por medio de la matemática aplicada o mediante programas
como la física computacional que elabora de modelos por ordenador de
sistemas con muchos grados de libertad. Las simulaciones se hacen resolviendo
sistemas de ecuaciones diferenciales ordinarias y en derivadas parciales. Como la dinámica
de las "partículas" suele ser aleatoria, se emplea método de Montecarlo.
Entre las aplicaciones más importantes están: física del estado sólido (magnetismo, estructura
electrónica, cambios de fase, etc.), física no lineal que se emplea, por
ejemplo, en simulaciones del Sistema Solar, y
física
de partículas utilizada en la teoría de campos/teoría gauge y especialmente en la Cromodinámica Cuántica (QCD).
La teoría de campos se
desarrolló, dentro de la mecánica cuántica, durante el siglo xix para
describir tanto al campo gravitatorio, el campo eléctrico así como otras formas
de materia continuas. La teoría cuántica de campos estudia la estructura de
la materia, siendo en la actualidad un campo de investigación muy
dinámico. La física ha encontrado una descripción bastante precisa de la
naturaleza basándose en la teoría cuántica de campos, hasta tal punto que la
mayoría de los físicos creen que la
realidad está hecha de campos cuánticos. Los campos son los componentes
fundamentales de la naturaleza, mientras que las partículas son excitaciones de
los campos. El principio de
incertidumbre de la mecánica cuántica afirma que en regiones muy pequeñas del
espacio todos los campos se encuentran fluctuando de forma continua y
anárquica. El vacío no está vacío; el espacio vacío está ocupado por campos. De
forma que: “No hay partículas sólo hay campos”. (Hobson, 2013).
Sin embargo, necesitan evidentemente de supercomputadoras, para visualizar esas fluctuaciones y poder realizar simulaciones físicas. Por otra parte, los ordenadores se basan en las estructuras elementales del Algebra de Boole. Un Algebra de Boole es una estructura matemática binaria (0 y 1) con tres operaciones lógicas: producto (AND), suma (OR) y Negación (NOT). Cualquier función lógica se puede realizar sólo con puertas NAND (producto negado) o sólo con puertas NOR (suma negada). Por ejemplo, la simulación mediante supercomputadoras es una función lógica. También la suma algebraica, es una función lógica. La solución de la ecuación de Schrödinger también es una función lógica. Una ecuación de ondas, es una función lógica, etc. En definitiva, cualquier simulación, que se realice en ordenadores, es una función lógica. Además, hay que tener en cuenta, que el encargado de realizar todas esas simulaciones y aplicaciones, es el microprocesador. Curiosamente el microprocesador es capaz de realizar muy pocas operaciones, en concreto, las operaciones que realiza se pueden resumir en: operaciones lógicas, tales como AND, OR y NOT y operaciones algebraicas como la suma aritmética, resta y comparación. En realidad la resta es una suma en complemento y la comparación es una resta, en la que el resultado no se guarda. En definitiva, se puede afirmar que la única operación matemática que realiza el microprocesador es la suma algebraica. Cualquier simulación, aplicación, algoritmo, incluso la Inteligencia Artificial, etc., no es más que un conjunto de sumas. La ecuación general de la suma es: S = x y, que físicamente se puede poner como c = w r. En donde c es la velocidad de la luz, r el radio de la partícula y w la velocidad de rotación.
El modelo desarrollado en este Blog parte de la hipótesis de que el espacio está formado por esferas de 4 dimensiones, cuyo diámetro es la longitud de Planck. Algunas de esas esferas giran (c=w r) dando lugar a las partículas con su propiedades y a las ecuaciones utilizadas tanto en mecánica cuántica como en relatividad especial y general.
En la tabla siguiente se da un resumen de las
ecuaciones deducidas a partir de la ecuación c = w r
· Principio de Incertidumbre de Heisenberg
· Ecuación de Schrödinger
· Gravitación de Newton
· Expresión General de la Fuerza a partir de la
cuál se deduce la:
o
Ley de
Lorentz, para el campo electromagnético y
o
Ley de
Lorentz para el campo gravitomagnético
§ Desviación del Perihelio de Mercurio
§ Desviación fotón en un Campo Gravitatorio
§ Contración Gravitacional de la Longitud
· Ecuaciones de Maxwell Generalizadas, que dan
lugar a:
o
Gravitomagnetismo
o
Electromagnetismo
o Ondas electromagnéticas y Gravitacionales
En este post vamos a ver las tres primeras.
Origen de la
Indeterminación de Heisenberg
El universo y
las partículas se rigen por una única ecuación:
c = w r (1)
Una ecuación y
dos incógnitas: la rotación w y el radio del disco plano que
constituye la partícula y que a su vez origina la onda que se observa. Por lo
tanto, la rotación w
no esta definida, excepto en los extremos, valores máximo y mínimo. El valor
máximo, corresponde a la rotación de Planck, y el mínimo que se corresponde con
un diámetro de la partícula igual a la longitud de onda Compton.
Los electrones
y quarks de primera generación poseen dos rotaciones. Una de las rotaciones es
alrededor de la cuarta dimensión, que origina el impulso o molesto lineal, y la
otra es la cuarta dimensión la que gira alrededor de dos ejes espaciales y que
da lugar a la carga y a la masa en reposo.
En los fotones,
la rotación alrededor de la cuarta dimensión es la que se observa como
frecuencia o longitud de onda, que corresponde al diámetro de la partícula. En
cambio la rotación de la cuarta dimensión es máxima y por lo tanto no se
observa, ya que corresponde al diametro de Planck
Se puede
considerar que tanto los electrones como los fotones, están formados por un
conjunto de esferas 4D de Planck que
giran ardedor de una de ellas. Por los tanto, debido a nuestra limitación
temporal, los electrones y fotones, son como discos planos giratorios, cuyo
diámetro es la longitud de onda reducida l/2p
y cuyo grosor es la longitud de Planck.
Figura
1 Representación tridimensional de electrones y fotones
Por lo tanto,
excepto en la circunferencia exterior, las esferas 4D de Planck giraran a una
velocidad v inferior a la de la luz, Luego, la ecuación (1) se puede poner:
Multiplicando por la constante reducida de Planck
Siendo
La energía de
la partícula utilizada en la observación y 1/w el periodo de rotación. De
manera que, cuando se utiliza, por ejemplo, un fotón de energía hc/l,
esta energía se transmite a la partícula observada, que aumenta su energía a la
vez que disminuye su periodo, luego la ecuación (3), se puede poner:
En realidad, lo
que se transmite es la rotación de una partícula a otra. De esta forma, la
partícula aumenta su rotación y disminuye su diámetro, y la ecuación (1) se
transforma en:
Lo que
imposibilita la medición de cualquier par de parámetros cuyo producto sea la
constante reducida de Planck.
Si
Δw es grande la energía o el
impulso de la partícula observada aumenta mucho, en cambio su radio varía poco.
Por el contrario, si Δw es pequeño la energía o el
impulso de la partícula observada aumenta poco, en cambio su radio varía mucho.
En definitiva, no se puede medir simultáneamente impulso y posición o energía y
tiempo. Ello es debido a que la constante reducida de Planck, es un factor de
conversión que transforma la rotación del fotón en energía (ħw), y la rotación del electrón
en masa (m=ħw/c^2) o en impulso (mvr=ħ). En
definitiva, la partícula observada, se adapta a las diferentes condiciones del
entorno modificando la rotación y el radio, pero manteniendo el producto de
ambos constante igual a la velocidad de la luz en el vacío.
Origen de la Gravitación de Newton
La gravitación de Newton y el principio de incertidumbre de Heisenberg son dos aspectos diferentes de la misma fórmula. Ambas fórmulas han sido obtenidas en épocas distintas y por métodos dispares, pero son la misma fórmula, ya que la Gravitación de Newton se deduce del principio de incertidumbre de Heisenberg.
La
ley de la gravitación de Newton, se deduce de la observación, mientras que la
relación de indeterminación de Heisenberg se deduce de los postulados de la
mecánica cuántica. Como ya ha sido publicada remito al lector al enlace
siguiente:
http://falaciascuanticas.blogspot.com/2014/11/deduccion-de-la-ley-de-la-gravitacion.html
Origen
de la Ecuación de Schrödinger
El electrón es una esfera 4D de
Planck con dos rotaciones. La rotación alrededor de la cuarta dimensión da
lugar al impulso (mv). Por lo tanto, el electrón, en cualquier átomo tendrá una
energía cinética (Ec=1/2
mv^2). Para ser observado, se
necesita por ejemplo fotones, los cuales tienen una rotación alrededor de la
cuarta dimensión. Dicha rotación se transmite al electrón de manera que al
aumentar la rotación, disminuye su área. Dicha área está formada por el radio
espacial y el radio en la cuarta dimensión, de manera que el tiempo
Figura 2. Área de observación
formada por la dirección de observación y la cuarta dimensión
Si definimos el tiempo al cuadrado
como la variación de la superficie para el cuadrado de la velocidad de la luz,
obtenemos: El tiempo será real y positivo para longitudes de onda largas (Fig.
2a)
y el tiempo será imaginario para
longitudes de onda cortas (Fig. 2b), longitudes de onda por debajo de la
longitud de onda del partícula.
La función de onda es la relación
de la energía cuando el electrón no es observado y cuando sí es observado.
Considere la función:
Ahora, basta con derivar con respecto al tiempo exterior y dos veces con respecto al espacio, para obtener la ecuación de Schrödinger para una partícula en reposo.
En física, un valor adimensional es un cociente entre magnitudes físicas, con distinto valor, pero con las mismas unidades, como por ejemplo la constante de estructura fina o la relación entre la masa del protón y lla del electrón o la constante de acoplamiento gravitacional. Pero una onda de probabilidad no tiene sentido físico, por eso la mecánica cuántica, aunque las ecuaciones funcionen es incomprensible, de ahí el famoso “Callate y Calcula.
Pero
una función de onda como cociente entre la energía que tiene el electrón y la
total que adquiere debida a la observación si tiene sentido físico.
https://www.ccsenet.org/journal/index.php/apr/article/view/0/41485





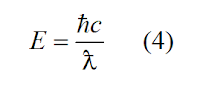

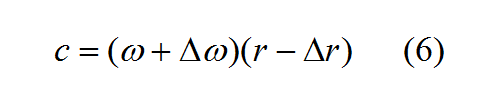


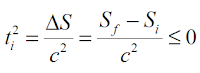

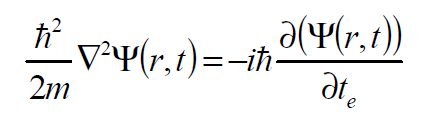
Un cordial saludo. Asumiendo que el tema tiene notable actualidad dado el reconocimiento académico que se están ganando los Programas de Inteligencia Artificial para consultas científico-técnicas, les cuento lo siguiente: consultamos simultáneamente 7 de estos programas sobre «el origen de la unidad de medida de la Constante de Planck» y resulta que todos coincidieron! en responder que «la unidad de medida de la Constante de Planck tiene implícito (es decir, conceptualmente su presencia es incuestionable pero académicamente ha sido ignorado desde sus inicios) un término en su denominador, y cuya presencia tiene implicaciones notables para la interpretación física de esta Constante»!. Entonces, ya que se trata de respuestas emitidas por estos programas y no por personas, debe resultar un «reto» muy interesante someterlos a escrutinio científico para determinar si «todos estos programas se equivocaron en su respuesta (lo que de por sí resultaría un hecho notable por las implicaciones para la credibilidad de estos programas I.A.) o por el contrario están en lo cierto!». Si les resulta de interés darle un «vistazo» hacédmelo saber a (diazreyesjosealberto62@gmail.com) para enviarles los textos. Atentamente, José Alberto
ResponderEliminar